本文目录
自然数的定义是什么
自然数是指用以计量事物的件数或表示事物次序的数。即用数码0,1,2,3,4……所表示的数。自然数由0开始,一个接一个,组成一个无穷的集体。
0是自然数吗
0是自然数,最小的自然数是0,没有最大的自然数。
自然数性质和特点
1、有序性。自然数的有序性是指,自然数可以从0开始,不重复也不遗漏地排成一个数列:0,1,2,3,…这个数列叫自然数列。
2、无限性。自然数集是一个无穷集合,自然数列可以无止境地写下去。
3、传递性:设n1,n2,n3都是自然数,若n1>n2,n2>n3,那么n1>n3。
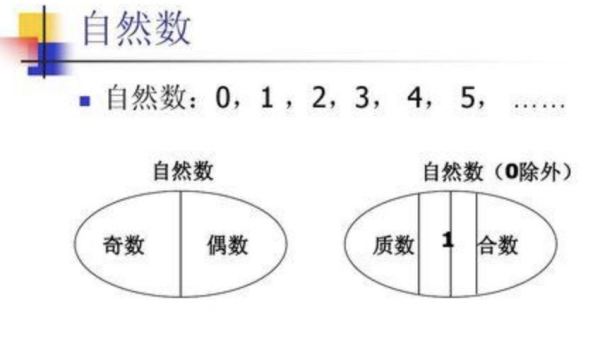
4、三岐性:对于任意两个自然数n1,n2,有且只有下列三种关系之一:n1>n2,n1=n2或n1 5、最小数原理:自然数集合的任一非空子集中必有最小的数。 数学运算定律 加法结合律 (a+b)+c=a+(b+c) 加法交换律 a+b=b+a 乘法结合律 (a*b)*c=a*(b*c) 乘法交换律 a*b=b*a 乘法分配律 a*(b+c)=a*b+a*c 1、自然数,是数学当中对于一类数字定下的性质概念,自然数是包含数字0在内的正整数的集合,我们也可以单独地将一个正整数称为自然数,自然数可以用来计量生活当中示事物的次序,亦或是件数,自然数有着无数个。 2、根据数字的奇偶性,我们又可以将自然数分为奇数和偶数这两个大类,数字0属于特殊的偶数。另外我们还可以将自然数称为是0、1、合数和质数的集合。所谓的合数指的就是能够被数字1余数值本身之外的数字(数字0除外)整除的正整数。质数指的就是只能够被数字1和本身数值(除了1和0)所整除的正整数. 3、任意的自然数一定属于是整数的,并且还一定是大于或者等于0的数。对于自然数的运算,在加法和乘法的运算当中,最后得出的结果一定是自然数,在减法和除法运算当中,最后得出的结果则不一定是自然数。 01 自然数是指表示物体个数的数,即由0开始,0,1,2,3,4…一个接一个,组成一个无穷的集体,即指非负整数。 自然数用以计量事物的件数或表示事物次序的数,即用0,1,2,3,4,……所表示的数。 自然数集是全体非负整数组成的集合,常用 N 来表示。自然数有无穷无尽的个数。(注:整数包括自然数,所以自然数一定是整数,且一定是非负整数。) 自然数集有加法和乘法运算,两个自然数相加或相乘的结果仍为自然数,也可以作减法或除法,但相减和相除的结果未必都是自然数,所以减法和除法运算在自然数集中并不是总能成立的。自然数是人们认识的所有数中最基本的一类,为了使数的系统有严密的逻辑基础,19世纪的数学家建立了自然数的两种等价的理论:自然数的序数理论和基数理论,使自然数的概念、运算和有关性质得到严格的论述。 (序数理论是意大利数学家G.皮亚诺提出来的。他总结了自然数的性质,用公理法给出自然数的如下定义) 自然数集N是指满足以下条件的集合: ①N中有一个元素,记作1。 ②N中每一个元素都能在 N 中找到一个元素作为它的后继者。 ③1是0的后继者。④0不是任何元素的后继者。 ⑤不同元素有不同的后继者。 ⑥(归纳公理)N的任一子集M,如果1∈M,并且只要x在M中就能推出x的后继者也在M中,那么M=N。 基数理论则把自然数定义为有限集的基数,这种理论提出,两个可以在元素之间建立一一对应关系的有限集具有共同的数量特征,这一特征叫做基数 。这样 ,所有单元素集{x},{y},{a},{b}等具有同一基数 , 记作1 。类似,凡能与两个手指头建立一一对应的集合,它们的基数相同,记作2,等等 。自然数的加法 、乘法运算可以在序数或基数理论中给出定义,并且两种理论下的运算是一致的。 自然数在日常生活中起了很大的作用,人们广泛使用自然数。自然数是人类历史上最早出现的数,自然数在计数和测量中有着广泛的应用。人们还常常用自然数来给事物标号或排序,如城市的公共汽车路线,门牌号码,邮政编码等。 自然数是整数(自然数包括正整数和零),但整数不全是自然数,例如:-1 -2 -3......是整数 而不是自然数。自然数是无限的。 全体非负整数组成的集合称为非负整数集,即自然数集。 在数物体的时候,数出的1.2.3.4.5.6.7.8.9……叫自然数。自然数有数量、次序两层含义,分为基数、序数。 基本单位:计数单位:个、十、百、千、万、十万...... 总之,自然数就是指大于等于0的整数。当然,负数、小数、分数等就不算在其内了。 自然数分类 按是否是偶数分 可分为奇数和偶数。 1、奇数:不能被2整除的数叫奇数。 2、偶数:能被2整除的数叫偶数。也就是说,除了奇数,就是偶数 注:0是偶数。(2002年国际数学协会规定,零为偶数.我国2004年也规定零为偶数。偶数可以被2整除,0照样可以,只不过得数依然是0而已)。 按因数个数分 可分为质数、合数、1和0。 1、质 数:只有1和它本身这两个因数的自然数叫做质数。也称作素数。 2、合 数:除了1和它本身还有其它的因数的自然数叫做合数。 3、1:只有1个因数。它既不是质数也不是合数。 4、当然0不能计算因数,和1一样,也不是质数也不是合数。 备注:这里是因数不是约数。 自然数是指用以计量事物的件数或表示事物次序的数。即用数码0,1,2,3,4……所表示的数。自然数由0开始,一个接一个,组成一个无穷的集体,自然数有有序性,无限性。分为偶数和奇数,合数和质数等。 但相减和相除的结果未必都是自然数,所以减法和除法运算在自然数集中并不总是成立的。用以计量事物的件数或表示事物次序的数,即用数码0,1,2,3,4,……所表示的数。 扩展资料: 自然数集合的任一非空子集中必有最小的数。具备性质3、4的数集称为线性序集。容易看出,有理数集、实数集都是线性序集。 例如所有形如nm(m>n,m,n 都是自然数)的数组成的集合是有理数集的非空子集,这个集合就没有最小数;开区间(0,1)是实数集合的非空子集,它也没有最小数。 以上就是关于自然数的定义 自然数是指什么,自然数的定义是什么的全部内容,以及自然数的定义 自然数是指什么的相关内容,希望能够帮到您。 版权声明:本文来自用户投稿,不代表【蒲公英】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。什么是自然数定义简单
自然数的定义是什么
自然数的定义是什么