本文目录
特征选择
特征选择主要的两个功能:
pearson Correlation :皮尔森相关系数是一种最简单的,能帮助理解特征和响应变量之间线性相关性,结果取值区间为[-1,1],-1表示完全地负相关,+1表示完全地正相关,0表示没有线性相关。
互信息和最大信息系数(Mutual information and maximal information coefficient)
想把互信息直接用于特征选择其实不太方便:
最大信息系数克服了这两个问题,它首先寻找一种最优的离散化方式,然后把互信息取值转换成一种度量方式,取值区间在[0,1]
ps: MIC的统计能力遭到了一些质疑,当零假设不成立时,MIC的统计就会受到影响。在有的数据集上不存在这个问题,但有的数据集上就存在这个问题。
距离相关系数法(Distance correlation)
距离相关系数是为了克服Pearson相关系数的弱点而生的,即使Pearson相关系数是0,我们也不能断定这两个变量是独立的(有可能是非线性相关);但如果距离相关系数是0,那么我们就可以说这两个变量时独立的。
尽管有MIC和距离相关系数在了,但当变量之间的关系接近线性相关的时候,Pearson相关系数任然是不可替代的。第一、Pearson相关系数计算速度快,这在处理大规模数据的时候很重要;第二、Pearson相关系数的取值区间是[-1,1],而MIC和距离系数都是[0,1],这个特点使得Pearson相关系数能够表征更丰富的关系,符号表示关系的正负,绝对值能够表示强度。当然,Pearson相关性有效的前提是两个变量的变化关系的单调的。
基于学习模型的特征排序(Model based ranking)
如何用回归模型的系数来选择特征,越是重要的特征在模型中对应的系数就会越大,而跟输出变量越是无关的特征对应的系数就会越接近于0,在噪音不多的数据上,或者是数量远远大于特征数的数据上,如果特征之间相对来说是比较独立的,那么即使是运用最简单的线性回归模型也一样能取得非常好的效果。
正则化
正则化就是把额外的约束或者惩罚项加到已有模型(损失函数)上,以防止过拟合并提高泛化能力。
L1正则化和L2正则化也称为Lasso和Ridge
L1正则化(Lasso)
L1正则化将系数w的L1范数作为惩罚项加到顺势函数上,由于正则项非零,这就迫使那些弱的特征所对应的系数变为0,因为L1正则化往往会使学到的模型很稀疏(系数w经常为0),这个特性使得L1正则化作为一种很好地特征选择方法。
L1正则化非正则化线性模型一样也是不稳定的,如果特征集合中具有相关联的特征,当数据发生细微变化时也有可能导致很大的模型差异。
L2正则化(Ridge regression)
L2正则化将系数向量的L2范数添加到了损失函数中。由于L2惩罚项中系数是二次方的,这使得L2和L1有着诸多差异,最明显的一点就是,L2正则化会让系数的取值变得平均。对于关联特征,这意味着他们能够获得更相近的对应系数。还是以Y=X1+X2为例,假设X1和X2具有很强的关联,如果用L1正则化,不论学到的模型是Y=X1+X2还是Y=2X1,惩罚都是一样的,都是2alpha。但是对于L2来说,第一个模型的惩罚项是2alpha,但第二个模型的是4*alpha。可以看出,系数之和为常数时,各系数相等时惩罚是最小的,所以才有了L2会让各个系数趋于相同的特点。
可以看出,L2正则化对于特征选择来说一种稳定的模型,不像L1正则化那样,系数会因为细微的数据变化而波动。所以L2正则化和L1正则化提供的价值是不同的,L2正则化对于特征理解来说更加有用:表示能力强的特征对应的系数是非零。
随机森林具有准确率高、鲁棒性好、易于使用等优点,这使得它成为了目前最流行的机器学习算法之一。随机森林提供了两种特征选择的方法:mean decrease impurity 和 mean decrease accuracy。
平均不纯度减少(mwan decrease impurity)
随机森林由多个决策树构成。决策树中每一个节点都是关于某一个特征的条件,为的是将数据集按照不同的响应变量一分为二。利用不纯度可以确定节点(最优条件),对于分类问题,通常采用基尼不纯度或者信息增益,对于回归问题,通常采用的是方差或者最小二乘拟合。当训练决策树的时候,可以计算出每个特征减少了多少树的不纯度,对于一个决策树森林来说,可以算出每个特征平均减少了多少不纯度,并把它平均减少的不纯度作为特征选择的值。
这里特征得分实际上采用的是Gini Importance。使用基于不纯度的方法的时候,要记住:1.这种方法存在偏向,对具有更多类别的变量会更有利;2.对于存在关联的多个特征,其中任意一个都可以作为指示器(优秀的特征),并且一旦某个特征被选择之后,其他特征的重要程度会急剧下降,因为不纯度已经被选中的哪个特征降下来了,其他的特征就很难再降低那么多不纯度了,这样一来,只有先被选中的那个特征很重要,而其余的特征是不重要的,但实际上这些特征对响应变量的作用确定非常接近的。
平均精确率减少(Mean decrease accuracy)
特征选择方法就是直接度量每个特征对模型精确度的影响。主要思路是打乱每个特征的特征值顺序,并且度量顺序变动对模型的精确率的影响。很明显,对于不重要的变量来说,打乱顺序对模型的精确率影响不会太大,但是对于重要的变量来说,打乱顺序就会降低模型的精确率。
建立在基于模型的特征选择方法基础之上的,例如回归和SVM,在不同的子集上建立模型,然后汇总最终确定特征得分。
稳定性选择(Stability selection)
稳定性选择是一种基于二次抽样和选择算法相结合较新的方法,选择算法可以是回归,SVM或者类似的方法。它的主要思想是在不同的数据子集和特征子集上运行特征选择算法,不断的重复,最终汇总特征选择结果。比如可以统计某个特征被认为是重要特征的频率(被选为重要特征的次数除以它所在的子集被测试的次数)。理想的情况下,重要特征的得分会接近100%。稍微弱一点的特征得分会是非零的数,而最无用的热证得分将会接近于0.
sklearn在随机lasso和随机逻辑回归中有对稳定性选择的实现。
递归特征消除(Recursive feature elimination RFE)
递归特征消除的主要思想是反复的构建模型(如SVM或者回归模型)然后选出最好的(或者最差的)的特征(可以根据系数来选),把选出来的特征放到一遍,然后在剩余的特征上重复这个过程,直到所有特征都遍历了,这个过程中特征被消除的次序就是特征的排序,因此,这是一种寻找最优特征子集的贪心算法。
RFE的稳定性很大程度上取决于在迭代的时候底层采用哪种模型。例如,假如RFE采用的普通的回归,没有经过正则化的回归是不稳定的,那么RFE就是不稳定的,假如采用的是Ridge,而用Ridge正则化的回归是稳定的,那么RFE就是稳定的。
Sklearn提供了RFE包,可以用于特征消除,还提供了RFECV,可以通过交叉验证来对特征进行排序。
l和l2损失函数与正则的区别是什么
作为损失函数:
L1 也被称为最小绝对值偏差(LAD),最小绝对值误差(LAE)。它是使目标值与预测值的绝对值总和最小化
L2范数损失函数,也被称为最小平方误差(LSE)。它是目标值和预测值平方差的最小化。
作为损失函数 L1和L2的区别如下:
作为正则化:
在机器学习中,正规化是防止过拟合的一种重要技巧。从数学上讲,它会增加一个正则项,防止系数拟合得过好以至于过拟合。L1与L2的区别只在于,L2是权重的平方和,而L1就是权重的和。如下:
他们的性质和区别:
内置特征选择是L1范数被经常提及的有用的性质,而L2范数并不具备。这是L1范数的自然结果,它趋向于产生稀疏的系数(在后面会解释)。假设模型有100个系数,但是仅仅只有其中的10个是非零的,这实际上是说“其余的90个系数在预测目标值时都是无用的”。L2范数产生非稀疏的系数,因此它不具备这个性质。
稀疏性指的是一个矩阵(或向量)中只有少数的项是非零的。L1范数具备性质:产生许多0或非常小的系数和少量大的系数。
计算效率。L1范数没有一个解析解,但是L2范数有。这就允许L2范数在计算上能高效地计算。然而,L1范数的解具备稀疏性,这就允许它可以使用稀疏算法,以使得计算更加高效。
l1 l2正则化
正则化(Regularization)是机器学习中一种常用的技术,其主要目的是控制模型复杂度,减小过拟合。最基本的正则化方法是在原目标(代价)函数 中添加惩罚项,对复杂度高的模型进行“惩罚”。其数学表达形式为:
其中, 为训练样本以及标签, 为目标函数, 为权重系数向量, 为惩罚项, 为惩罚因子。不同的 对权重 的最优解有不同的偏好,因而会产生不同的正则化效果。最常用的是 范数和 范数,相应称之为 正则和 正则。
深入理解L1、L2正则化 从带约束条件的优化求解和最大后验概率两种思路对L1、L2正则化给出了分析。本文从只说下带约束条件的优化求解(因为目前我只能理解这种思路。。。)
我们知道,模型的复杂度可用VC维来衡量。通常情况下,模型VC维与系数 的个数成线性关系:即 数量越多,VC维越大,模型越复杂。因此,为了限制模型的复杂度,很自然的思路是减少系数 的个数,即让 向量中一些元素为0或者说限制 中非零元素的个数。为此,我们可在原优化问题中加入一个约束条件:
范数表示向量中非零元素的个数。但由于该问题是一个NP问题,不易求解,为此我们需要稍微“放松”一下约束条件。为了达到近似效果,我们不严格要求某些权重 为0,而是要求权重 应接近于0,即尽量小。从而可用 范数和 范数来近似 ,即:
利用拉格朗日算子法,我们可将上述带约束条件的最优化问题转换为不带约束项的优化问题,构造拉格朗日函数:
综上所述, 正则和 正则是通过将某些 为0或者接近于0,降低模型复杂度,防止过拟合。
当 为1维的时候, 和 的函数图像如下:
和 , 会向0的方向优化;区别在于, 中 将不会再变化,而 是接近于0但不会等于0(个人想法)。
《深度学习》第七章(7.1--7.2)有公式推导,有时间可以再好好看看,初看没看懂。
l1正则项和l2的区别
L1,L2正则都可以看成是 条件限制,即
∥w∥≤c
∥w∥2≤c
当w为2维向量时,可以看到,它们限定的取值范围如下图:
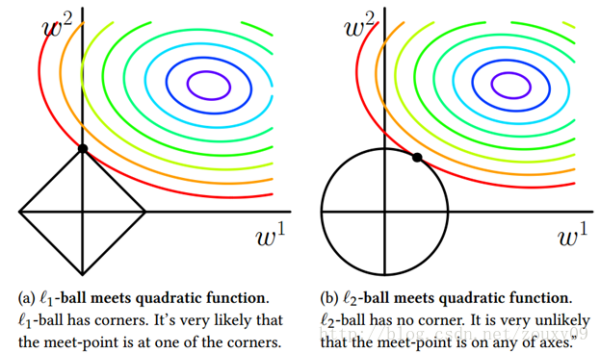
所以它们对模型的限定不同
而对于一般问题来说,L1 正则往往取到正方形的顶点,即会有很多分量为0,具有稀疏性,有特征选择的作用
以上就是关于l和l2正则化的区别,特征选择的全部内容,以及l1和l2正则化的区别的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【蒲公英】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。