本文目录
导函数连续的充要条件是什么
解:
x→0+
lim|sinx|=limsinx=0=sin0
x→0-
limsinx=lim-sinx=0=sin0
左右都连续.所以连续
x→0+
lim(|sinx|-|sin0)|/(x-0)=limsinx/x=1
x→0-
lim(|sinx|-|sin0)|/(x-0)=lim-sinx/x=-1
左右导数不等,所以不可导。
连续性:y在X的领域内处有定义,而且y在X趋向于0时极限存在,而且极限值等于y在X=0的值。证明极限存在,要看左右极限是否存在且相等,像这函数,左右极限都存在,且都等于0,而且极限值等于函数值。
可导性:先对函数进行求导,再求其在X=0处左右极限是否存在且相等,如果不存在,则不可导,如果存在可是不相等,也不可导。
扩展资料
函数的连续性:
在定义函数的连续性之前先了解一个概念——增量设变量x从它的一个初值x1变到终值x2,终值与初值的差x2-x1就叫做变量x的增量,记为:△x即:△x=x2-x1增量△x可正可负。
设函数在区间[a,b)内有定义,如果右极限存在且等于,即:=,那么就称函数在点a右连续。一个函数在开区间(a,b)内每点连续。
则为在(a,b)连续,若又在a点右连续,b点左连续,则在闭区间[a,b]连续,如果在整个定义域内连续,则称为连续函数。
注:一个函数若在定义域内某一点左、右都连续,则称函数在此点连续,否则在此点不连续。注:连续函数图形是一条连续而不间断的曲线。
连续的充要条件是什么
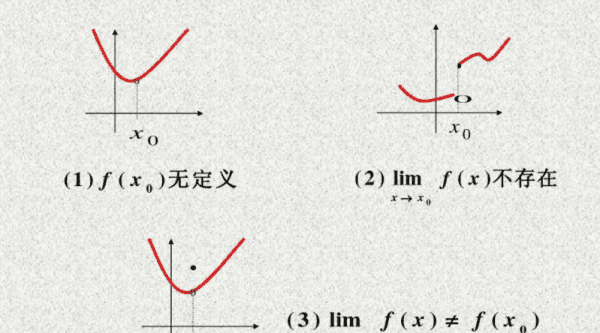
判断函数f(x)在x0点处连续,当且仅当f(x)满足以下三个充要条件:
1、f(x)在x0及其左右近旁有概念。
2、f(x)在x0的极限存在。
3、f(x)在x0的极限值与函数值f(x0)相等。
简介
所有多项式函数都是连续的。各类初等函数,如指数函数、对数函数、平方根函数与三角函数在它们的定义域上也是连续的函数。
绝对值函数也是连续的。定义在非零实数上的倒数函数f= 1/x是连续的。但是如果函数的定义域扩张到全体实数,那么无论函数在零点取任何值,扩张后的函数都不是连续的。
函数连续的充要条件
函数连续的充要条件是:如果函数f在点a连续,那么f在点a的左极限、右极限和函数值都存在且相等
1、如果函数f在点a连续,那么f在点a的左极限、右极限和函数值都存在且相等即lim_(x->a-)f(x)=f(a)=lim_(x->a+)f(x)。这就是所谓的“三合一”原则。
2、函数的连续性是数学分析中的一个重要概念,它描述了函数在某一点或某一区间内的性质。一个函数在某个点连续,意味着函数在该点的极限存在且等于函数值;如果函数在区间内的每一点都连续,那么这个函数就是在整个区间上连续的。

3、如果函数f在区间(a,b)上连续,那么f在区间端点的值相等,即f(a)=f(b)。同时,如果函数f在区间(a,b)上连续,且在开区间(a,b)内可导,那么f在区间(a,b)上必定可积。
函数的相关信息
1、函数是数学中的一种基本概念,它描述了两个量之间的依赖关系。在函数中,一个量被称为自变量,另一个量被称为因变量或函数值。函数通常用符号f来表示,自变量的取值范围称为定义域,函数值的取值范围称为值域。
2、函数可以是一元函数,即只涉及一个自变量和一个因变量;也可以是多元函数,即涉及多个自变量和多个因变量。函数还可以是离散的或连续的。离散函数在其定义域内的任意两点之间都有定义,而连续函数在其定义域内的每一点都有定义。

3、函数的概念在数学、物理、工程等许多领域都有广泛的应用,例如,物理学中的力和加速度之间的关系可以用函数来描述;经济学中的供求关系也可以用函数来表示。此外,函数还是计算机科学中的重要概念,许多编程语言都提供了对函数的支持。
函数连续的条件是什么
1、充分条件:若函数f(x)在x0可导或可微(或者更强的条件),则函数在x0连续。
2、必要条件:若函数f(x)在x0无定义、或无极限、或极限不等于函数值,则在x0不连续。
3、若函数f(x)在x0有定义,且极限与函数值相等。则函数在x0连续。
4、连续函数的法则:定理一:在某点连续的有限个函数经有限次和、差、积、商(分母不为0) 运算,结果仍是一个在该点连续的函数。定理二:连续单调递增 (递减)函数的反函数,也连续单调递增 (递减)。定理三:连续函数的复合函数是连续的。

以上就是关于函数连续的充要条件,导函数连续的充要条件是什么的全部内容,以及函数连续的充要条件的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【蒲公英】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。










