本文目录
程序中的栈和队列是什么意思啊
栈(Stack)是仅限制在表的一端进行插入和删除运算的线性表,称插入、删除这一端为栈顶,另一端称为栈底。表中无元素时为空栈。栈
的修改是按后进先出的原则进行的,我们又称栈为LIFO表(Last
In
First
Out)。通常栈有顺序栈和链栈两种存储结构。
栈的基本运算有六种:
·构造空栈:InitStack(S)
·判栈空:
StackEmpty(S)
·判栈满:
StackFull(S)
·进栈:
Push(S,x)
·退栈:
Pop(S)
·取栈顶元素:StackTop(S)
在顺序栈中有"上溢"和"下溢"的现象。
·"上溢"是栈顶指针指出栈的外面是出错状态。
·"下溢"可以表示栈为空栈,因此用来作为控制转移的条件。
顺序栈中的基本操作有六种:·构造空栈·判栈空·判栈满·进栈·退栈·取栈顶元素
链栈则没有上溢的限制,因此进栈不要判栈满。链栈不需要在头部附加头结点,只要有链表的头指针就可以了。
链栈中的基本操作有五种:·构造空栈·判栈空·进栈·退栈·取栈顶元素
队列(Queue)是一种运算受限的线性表,插入在表的一端进行,而删除在表的另一端进行,允许删除的一端称为队头(front),允许插入的
一端称为队尾(rear)
,队列的操作原则是先进先出的,又称作FIFO表(First
In
First
Out)
。队列也有顺序存储和链式存储两种存储结
构。
队列的基本运算有六种:
·置空队:InitQueue(Q)
·判队空:QueueEmpty(Q)
·判队满:QueueFull(Q)
·入队:EnQueue(Q,x)
·出队:DeQueue(Q)
·取队头元素:QueueFront(Q)
顺序队列的"假上溢"现象:由于头尾指针不断前移,超出向量空间。这时整个向量空间及队列是空的却产生了"上溢"现象。
为了克服"假上溢"现象引入循环向量的概念,是把向量空间形成一个头尾相接的环形,这时队列称循环队列。
判定循环队列是空还是满,方法有三种:
·一种是另设一个布尔变量来判断;
·第二种是少用一个元素空间,入队时先测试((rear+1)%m
=
front)?
满:空;
·第三种就是用一个计数器记录队列中的元素的总数。
队列的链式存储结构称为链队列,一个链队列就是一个操作受限的单链表。为了便于在表尾进行插入(入队)的操作,在表尾增加一个尾指
针,一个链队列就由一个头指针和一个尾指针唯一地确定。链队列不存在队满和上溢的问题。在链队列的出队算法中,要注意当原队中只
有一个结点时,出队后要同进修改头尾指针并使队列变空。
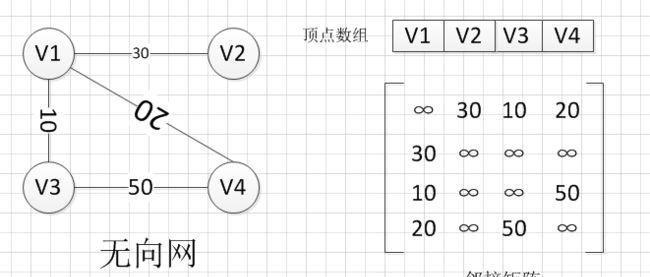
数据结构总结与心得
第三章栈和队列
栈
栈的定义及基本运算
栈是限制仅在表的一端进行插入和删除运算的线性表又称为后进先出表(LIFO表) 插入 删除端称为栈顶 另一端称栈底 表中无元素称空栈 基本运算有
) initstack(s) 构造一个空栈;
) stackempty(s) 判栈空;
) stackfull(s) 判栈满;
) push(s x) 进栈;
) pop (s) 退栈;
) stacktop(s) 取栈顶元素
顺序栈
栈的顺序存储结构称顺序栈 顺序栈的类型定义为
#define stacksize
typedef char datatype;
typedef struct{
datatype data[stacksize];
int top;
}seqstack;
当栈满时 做进栈运算必定产生空间溢出 称 上溢 当栈空时 做退栈运算必定产生空间溢出 称 下溢 上溢是一种错误应设法避免 下溢常用作程序控制转移的条件
在顺序栈上的基本运算
) 置空栈
Void initstack(seqstack *s)
{
s >top= ;
}
)判栈空
int stackempty(seqstack *s)
{
return s >top== ;
}
)判栈满
int stackfull(seqstack *s)
{
return s >top==stacksize ;
}
)进栈
Void push(seqstack *s datatype x)
{
if(stackfull(s))
error( stack overflow );
s >data[++s >top]=x;
}
)退栈
Datatype pop(seqstack *s)
{
if(stackempty(s))
error( stack underflow );
return S >data[s >top ];
}
)取栈顶元素
Dtatatype stacktop(seqstack *s)
{
if(stackempty(s))
error( stack underflow );
return S >data[s >top];
}
链栈
栈的链式存储结构称链栈 栈顶指针是链表的头指针 链栈的类型定义
typedef struct stacknode{
datatype data;
struct stacknode *next;
}stacknode;
typedef struct{
stacknode *top;
}linkstack;
链栈上的基本运算
) 建栈
Void initstack(linkstack *s)
{
s >top=NULL;
}
)判栈空
Int stackempty (linkstack *s)
{
return s >top==NULL;
}
) 进栈
Void push(linkstack *s datatype x)
{
stacknode *p=(stacknode *)malloc(sizeof(stacknode));
p >data=x;
p >next=s >top;
s >top=p;
}
) 退栈
Datatype pop(linksatck *s)
{
datatype x;
stacknode *p=s >top;
if(stackempty(s))
error( stack underflow );
x=p >data;
s >top=p >next;
free(p);
return x;
}
) 取栈顶元素
Datatype stacktop(linkstack *s)
{
if(stackempty(s))
error( stack is empty );
return s >top >data;
}
队列
队列的基本定义和计算
队列是一种运算受限的线性表 允许删除的一端称队首 允许插入的一端称队尾 队列又称为先进先出线性表 FIFO表
队列的基本运算
) initqueue(q) 置空队;
) queueempty(q) 判队空;
) queuefull(q) 判队满;
) enqueue(q x) 入队;
) dequeue(q) 出队;
) queuefront(q) 返回队头元素
顺序队列
队列的顺序存储结构称顺序队列 设置front和rear指针表示队头和队尾元素在向量空间的位置 顺序队列中存在 假上溢 现象 由于入队和出队操作使头尾指针只增不减导致被删元素的空间无法利用 队尾指针超过向量空间的上界而不能入队
为克服 假上溢 现象 将向量空间想象为首尾相连的循环向量 存储在其中的队列称循环队列 i=(i+ )%queuesize
循环队列的边界条件处理 由于无法用frOnt==rear来判断队列的 空 和 满 解决的方法有
) 另设一个布尔变量以区别队列的空和满;
) 少用一个元素 在入队前测试rear在循环意义下加 是否等于front;
) 使用一个记数器记录元素总数
循环队列的类型定义
#define queuesize
typedef char datatype;
typedef struct{
int front;
int rear;
int count;
datatype data[queuesize];
}cirqueue;
) 置队空
Void initqueue(cirqueue *q)
{
q >frOnt=q >rear= ;
q >count= ;
}
) 判队空
Int queueempty(cirqueue *q)
{
return q >count== ;
}
) 判队满
Int queuefull(cirqueue *q)
{
return q >count==queuesize;
}
) 入队
Void enqueue(cirqueue *q datatype x)
{
if(queuefull(q))
error( queue overfolw );
q >count++;
q >data[q >rear]=x;
q >rear=(q >rear+ )%queuesize;
}
) 出队
Datatype dequeue(cirqueue *q)
{
datatype temp;
if(queueempty(q))
error( queue underflow );
temp=q >data[q >front];
q >count ;
q >frOnt=(q >front+ )%queuesize;
return temp;
}
) 取队头元素
Datatype queuefront(cirqueue *q)
{
if(queueempty(q))
error( queue is empty );
return q >data[q >front];
}
链队列
队列的链式存储结构称链队列 链队列由一个头指针和一个尾指针唯一确定
链队列的定义
typedef struct queuenode
{
datatype data;
struct queue *next;
}queuenode;
typedef struct
{
queuenode *front;
queuenode *rear;
}linkqueue;
) 建空队
Void initqueue(linkqueue *q)
{
q >frOnt=q >rear=NULL;
}
) 判队空
Int queueempty(linkqueue *q)
{
return q >frOnt==NULL&&q >rear==NULL;
}
) 入队
Void enqueue(linkqueue *q datatype x)
{
queuenode *p=(queuenode *)malloc(sizeof(queuenode));
p >data=x;
p >next=NULL;
if(queueempty(q))
q frOnt=q >rear=p;
else{
q >rear >next=p;
q >rear=p;
}
}
) 出队
Datatype dequeue(linkqueue *q)
{
datatype x;
queuenode *p;
if(queueempty(q))
error( queue is underflow );
p=q >front;
x=p >data;
q >frOnt=p >next;
if(q >rear==p) q >rear=NULL;
free(p);
return x;
}
) 取队头元素
Datatype queuefront(linkqueue *q)
{
if(queueempty(q))
error( queue is empty );
return q >front >data;
}
附二:
第三章 栈和队列
*************************************************************************************
栈(Stack)是仅限制在表的一端进行插入和删除运算的线性表 称插入 删除这一端为栈顶 另一端称为栈底 表中无元素时为空栈 栈的修改是按后进先出的原则进行的 我们又称栈为LIFO表(Last In First Out) 通常栈有顺序栈和链栈两种存储结构
*************************************************************************************
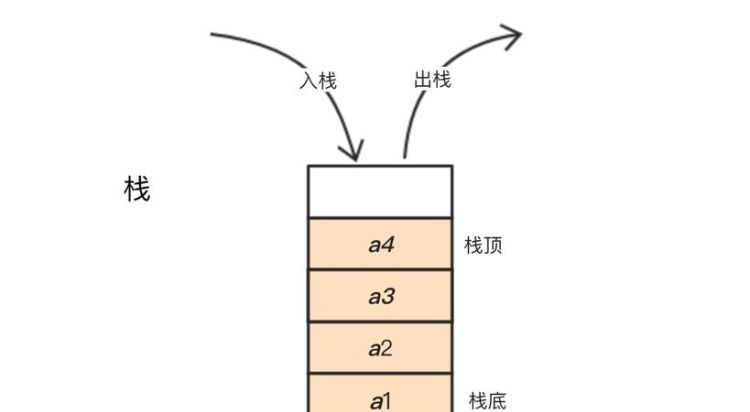
栈是什么的线性表,其运算遵循
栈(stack)是一个特殊的线性表,是限定在一端(通常是表尾)进行插入和删除操作的线性表。又被称作后进先出(LastInFirstOut)的线性表,简称LIFO结构。
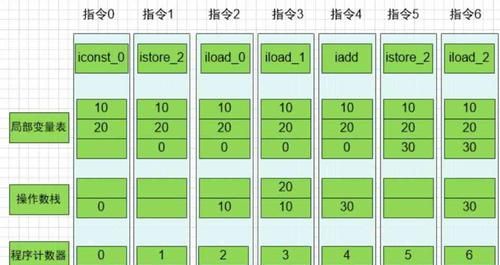
计算机中的栈是什么
计算机中的栈是一种运算受限的线性表。
栈(stack)又名堆栈,它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
栈可以用来在函数调用的时候存储断点,做递归时要用到栈。在i386机器中,栈顶由称为esp的寄存器进行定位。压栈的操作使得栈顶的地址减小,弹出的操作使得栈顶的地址增大。
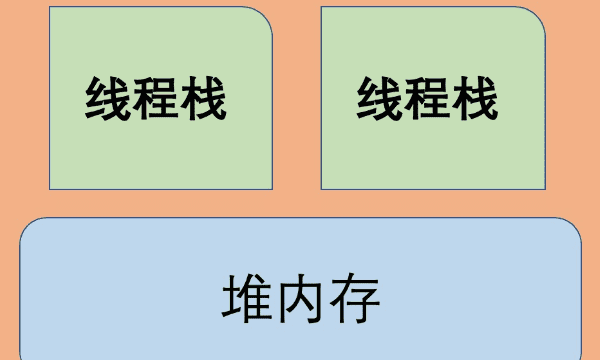
栈的作用
1、保存局部变量:函数里面也有可能要使用到局部变量,而不能总是用全局变量。则局部变量存储到哪里合适,即不能让函数嵌套的时候有冲突,又要注重效率。
2、参数传递:传递参数的目的,是为了代码可以重用,让一种方法可以应用到更多的场合,而不需要为N种情况写N套类似的代码。
3、保存寄存器的值:寄存器传参的冲突,可以把寄存器的值临时压入栈里面。
4、其他作用:栈是每个函数架构的基础,实现了函数的重复利用。问题发生的时候,可以利用栈来了解问题发生的情况。栈是构建出操作系统多任务模式的基础。
以上就是关于栈经常被称为什么表,程序中的栈和队列是什么意思的全部内容,以及栈经常被称为什么表的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【蒲公英】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。


