本文目录
函数连续性和可导性之间有什么关联吗
函数连续性和可导性的关系如下:
连续的函数不一定可导;可导的函数是连续的函数;越是高阶可导函数曲线越是光滑;存在处处连续但处处不可导的函数。
拓展资料
函数的连续性和可导性是微积分中两个重要的概念。连续性是指函数在定义域内不存在跳跃或断裂的情况,而可导性则是指函数在某一点处存在切线斜率的概念。
一个函数在某一点处连续,意味着当自变量趋近于该点时,函数值也趋近于该点对应的函数值。换句话说,函数值的变化是平稳、连续的。形式化地,对于函数f(x),如果对于定义域内的任意x=a,当x趋近于a时,f(x)也趋近于f(a),那么可以说函数f(x)点a处连续。

一个函数在某一点处可导,意味着该点存在唯一的切线,并且切线的斜率存在。可导性与连续性有着密切的关系。具体来说,如果函数f(x)在某一点a处可导,那么函数f(x)在点a处必然连续。这是因为可导性要求函数在某一点的极限存在,并且极限值等于该点处的函数值,而连续性要求函数在该点的极限等于该点处的函数值。因此,可导性是连续性的一个更强的条件。
连续性不一定能够保证可导性。有些函数在某一点处连续,但在该点处没有切线斜率,因此不可导。例如,在函数f(x)=|x|中,当x=0时,虽然该函数在点x=0处连续,但由于左右导数不相等,不存在唯一的切线斜率,因此该函数在点x=0处不可导。
值得注意的是,当函数在某一点处可导时,它必然在该点处连续,但连续性并不保证可导性。这就意味着,函数的连续性是可导性的一个充分条件,但不是必要条件。

关于连续与可导的性质
1、连续性和可导性使得函数在数学建模和实际问题中具有重要的应用价值。连续性能够研究函数在定义域内的各种性质,如函数的极值、函数图像的形态等。可导性则提供了研究函数局部性质的工具,如切线斜率、导数的变化等。这些概念在物理学、经济学、工程学等学科中都得到广泛的应用。
2、连续函数的基本运算法则和可导函数的求导法则为求解函数的极限、最值、方程等问题提供了便利。通过对连续函数的性质和可导函数的导数进行分析,可以探索函数的特殊性质,并进一步解决实际问题。
3、连续性和可导性还与数学分析中的一些重要定理和概念相关。例如,连续函数的最值定理和介值定理等,以及可导函数的中值定理和泰勒展开等。这些定理和概念为研究函数的性质和求解各类问题提供了强有力的工具和方法。
连续与可导的关系是什么?可以举例说明
连续与可导的关系:
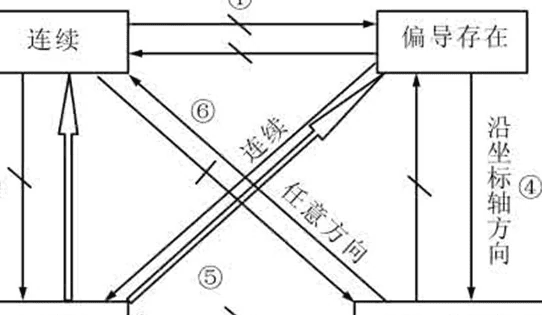
1、连续的函数不一定可导;
2、可导的函数是连续的函数;
3、越是高阶可导函数曲线越是光滑;
4、存在处处连续但处处不可导的函数。
可导:
微积分是在17世纪末由英国物理学家、数学家牛顿和德国数学家莱布尼茨建立起来的。微积分是由微分学和积分学两部分组成,微分学是基础。微分学的基本概念是导数和微分,核心概念是导数。导数反应了函数相对于自变量的变化率问题。
函数连续和可导的关系
函数连续和可导的关系是可导性一定意味着连续性。也就是说,如果一个函数在某点可导,那么它在该点也是连续的。
可导性:函数f(x)在点x处可导,意味着它在该点的导数存在,即导数极限
f′(x)=lim(h→0)[f(x+h)−f(x)]/h存在。
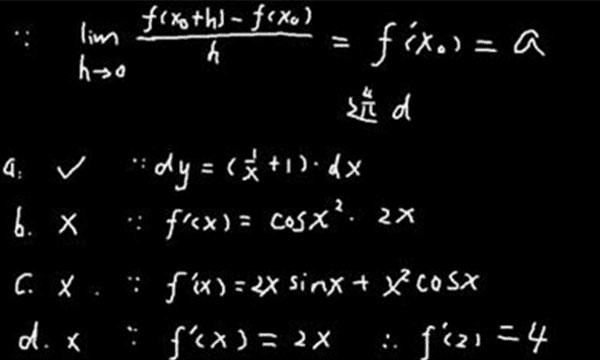
连续性:函数f(x)在点x处连续,意味着在该点的函数值与极限值相等,即
lim(x→a)f(x)=f(a)
如何判断一个函数可导?
导数的定义是这样的:函数y=f(x)在x。的某邻域内有定义。设在x。自变量x的改变量是Ax,相应函数的改变量是Ay=f(x。+Ax)-f(x。),如果Ay/Ax的极限(当Ax→0时)存在,称函数f(x)在点ⅹ。
可导(或存在导数),此极限称为函数f(x)在点x。的导数,记为f'(x。)。如果此极限不存在,称函数f(x)在点x。不可导。
函数在一点可导,则函数在这点连续。即《可导→连续》。但是若函数在一点连续,函数则在这点不一定可导。
一般的,幂函数,对数函数,指数函数,三角函数,反三角函数,双曲函数及常函数这些初等函数在其定义域内一般是可导的。但是,有些连续函数是不可导的,像一些分段函数,在段点处要仔细判断。
可导与连续的关系
可导与连续的关系是可导一定连续,连续不一定可导。
也就是说,如果一个函数在某点可导,那么这个函数在该点一定连续;但是如果一个函数在某点连续,那么这个函数在该点不一定可导。
这是因为连续是函数的取值,可导是函数的变化率。可导是更高一个层次。具体来说,存在处处连续但处处不可导的函数。左导数和右导数存在且相等,才是函数在该点可导的充要条件,不是左极限=右极限(左右极限都存在)。

可导与连续的关系是,在函数f(x)的某个点x处,如果f(x)可导,那么f(x)在x处连续。换句话说,如果一个函数在某个点的导数存在,那么这个函数在该点的值是连续的。
这个关系可以理解为,当函数在某点的导数存在时,说明函数在该点的变化率是有限的,不会出现跳跃或者不连续的情况。因此,函数在该点的值一定是连续的。
但是需要注意的是,这个关系并不意味着可导一定意味着连续。在某些情况下,函数可能在某些点处不可导,但仍然是连续的。例如,在函数f(x)=|x|在x=0处,由于f(0)=0,但f(0)不存在(因为在0处,函数没有切线),所以f(x)在x=0处不可导,但是f(x)在x=0处是连续的。
可导与连续的作用:
1、在数学中,可导和连续是微积分学的基础。微积分学是研究函数的变化率和极限的重要工具。在实际问题中,可导和连续可以用来描述物理现象的变化,例如速度和加速度的变化,以及热量的传导等。
2、在经济学中,可导和连续被广泛应用于最优化问题。例如,在研究一个企业的生产成本最小化问题时,需要用到函数的导数来确定最优的生产量。此外,连续函数的积分还可以用来计算总成本和总收益。

3、在计算机科学中,可导与连续也有重要的应用。例如,在机器学习和人工智能领域,梯度下降算法是一种常用的优化方法。该算法利用函数的导数来计算函数的最优解,因此函数的可导性和连续性对于梯度下降算法的收敛速度和精度都有重要的影响。
4、在自然科学和工程领域中,可导与连续也是非常重要的概念。例如,在物理学中,物体的运动规律通常可以用连续的函数来描述;在工程设计中,材料的强度和弹性往往需要考虑材料的连续性和可导性。
以上就是关于函数连续和可导的关系,函数连续性和可导性之间有什么关联的全部内容,以及函数连续和可导的关系的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【蒲公英】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。